Ralph Merkle et Martin Hellman, deux cryptographes américains présentent en 1978 un des premiers cryptosystèmes asymétriques. Cet article va présenter ce chiffrement puis décrira 3 différentes attaques contre celui-ci.
Présentation du cryptosystème:
Le schéma que propose R.Merkle et M.Hellman est un système reposant sur le problème du sac à dos.
C’est un système asymétrique ce qui veut dire qu’il est composé :
- d’une clé publique (chiffrement)
- d’une clé privée (Déchiffrement)
Problème du sac à dos :
Le problème du sac à dos et un problème d’optimisation combinatoire. L’idée est de maximiser la valeur totale des objets que vous pouvez mettre dans un sac à dos, tout en respectant sa capacité maximale. On vous donne une liste d’objets, chaque objet ayant une valeur et un poids. Le défi est de déterminer quels objets inclure dans le sac de manière à maximiser la valeur totale tout en ne dépassant pas la capacité du sac.
Knapsack
Le Knapsack Problem est un exemple particulier du problème du sac à dos appelé le problème de la somme de sous-ensembles.
En anglais subset sum problem, le problème de la somme des sous-ensembles peut être décrit de la manière suivante:
L’idée est de déterminer si, dans un ensemble donné de nombres, il existe un sous-ensemble dont la somme est égale à une valeur cible.
Exemple :
On considère un ensemble E
E=\{2,5,10,13,42,68,95,102,110,237,300,697,999,1843\}et un entier
T= 1469Le but est de trouver un sous ensemble de "E" tel que la somme des éléments de ce sous ensemble soit égale à "T".
La solution est ici
S=\{5,10,13,95,110,237,999\} \in E puisque
5+10+13+95+110+237+999=1469Ce problème est NP-Complet, c’est-à-dire qu’il est facile de vérifier rapidement toutes solutions proposées, mais qu’on ne sait pas en trouver efficacement. Chaque algorithme connu pour résoudre des problèmes NP-complets affiche une complexité temporelle exponentielle en fonction de la taille des données d’entrée, rendant ainsi leur utilisation presque impraticable, même pour des instances de taille modérée.
C’est en se basant sur ce constat de la difficulté à résoudre ce problème rapidement qu’on voit apparaître le cryptosystème de Merkle-Hellman .
Génération des clefs.
On choisit une séquence super-croissante U de taille n :
U = (u_1, u_2, ..., u_n)C’est une séquence d’entiers où chaque élément est strictement supérieur à la somme de tous les éléments précédents :
La suite U est super-croissante lorsque :
\forall n \in N, u_{n+1} > \sum_{i=0}^n u_iOn prend
A \in N ~tel~que~A~> \sum_{i=1}^n a_iPuis
w \in [1, A-1] ~|~ pgcd(w,A)=1On calcule la séquence B avec
b_i = u_i \times w \mod Apour chaque
i \in \{1,2,..,n\}On obtient ainsi :
- une clé publique :
\{b_1,b_2,...,b_n\} - une clé privée :
(A, w, \{a_1, a_2,.., a_n\})
Comme toute clé privée, cette dernière clé doit être tenue secrète afin de protéger le cryptosystème.
La raison de l’utilisation d’une suite super-croissante est qu’il est facile de résoudre le subset sum problem dans ce cas précis.
On peut coder la génération de clé de cette manière :
from Crypto.Util.number import long_to_bytes, bytes_to_long, getPrime, GCD
from Crypto.Util.Padding import pad, unpad
from Crypto.Cipher import AES
from random import randint
from hashlib import sha256
class Knapsack:
def __init__(self, size: int) -> None:
self.size = size
self.gen_key()
def gen_key(self, K:int = 5000) -> None:
# Génération du séquence super-croissante
U = []
for _ in range(self.size):
U.append(randint(sum(U)+ K + 1, 2 * (sum(U)+ K)))
# A > sum(u)
A = getPrime(sum(U).bit_length()+1)
# 2 < w < A-1 && pgcd(w,A) = 1
w = randint(2, A - 1)
while GCD(w, A) != 1:
w = randint(2, A - 1)
self.pub = [(u * w) % A for u in U]
self.priv = (A, w, U)Chiffrement.
On note m un message en clair, on convertit m en binaire afin d’avoir une séquence de bit:
m=(m_1, m_2, ...)On calcule le message chiffré grâce à la clé publique avec :
c=\sum_{i=1}^n m_i \times b_iExemple :
On pose n=10, et on génère la clé publique suivante :
U=\{63642, 37769, 75538, 24685, 118366, 90121, 68426, 28907, 70320, 101444\}Ainsi que la clé privée correspondante :
B=\{10, 21, 42, 147, 399, 1129, 2602, 6042, 13649, 33318\} \\
A = 119849 \\
w = 30334 \\Avec une clé de n éléments, on peut chiffrer des messages de 2**n bits maximum.
On souhaite chiffrer le message : m=419 :
On le convertit en binaire en paddant de 0 le résultat:
>>> bin(409)[2:].zfill(10)
'0110011001'On obtient donc :
m = (0,1,1,0,0,1,1,0,0,1)Finalement, on calcule:
C=0\times63642 + 1\times37769 + 1\times75538 + 0\times24685 + 0\times118366 + 1\times90121 + 1\times68426 + 0\times28907 + 0\times70320 + 1\times101444 \\ ~ \\
C = 373298On a en python:
def encrypt(self, m: int) -> int:
# Convertion en binaire + padding de 0
M = bin(m)[2:].zfill(self.size)
# Calcul de la somme
C = sum([ int(M[i]) * self.pub[i] for i in range(self.size)])
return CDéchiffrement
Afin de déchiffrer le message c, on calcule r, l’inverse modulaire de w modulo A :
r = w^{-1} \mod A(L’algorithme d’Euclide étendu peut ici être utilisé)
Ensuite, il suffit de calculer
c' = c*r \mod Ace qui donne :
c' \equiv c*r \equiv c*w^{-1} \equiv \sum_{i=1}^n x_i*b_i*w^{-1} \equiv \sum_{i=1}^n x_i*u_i \mod ALe sac à dos d’origine étant une séquence super-croissante, il est facile de retrouver la solution avec un algorithme glouton.
Exemple :
En reprenant l’exemple précédent, nous avions :
- C = 373298
On calcule r:
r = w^{-1} \mod A = 30334^{-1} \mod 119849 = 30063>>> pow(30334,-1,119849)
30063puis c’ :
c' = c \times r \mod m = 373298 \times 30063 \mod 119849 = 37112Enfin, on décompose c’:
37112=33318+2602+1129+1129+42+21et on retrouve :
37112 = 0\times10 + 1\times21 + 1\times42 + 0\times147 + 0\times399 + 1\times1129 +1\times2602 + 0\times6042 + 0\times13649 + 1\times33318Le message d’origine est donc : 0110011001
En python:
def decrypt(self, C: int) -> bytes:
A, w, U = self.priv
r = pow(w, -1, A)
c_prime = C*r % A
r = []
for i, u in enumerate(U[::-1]):
while c_prime >= u and u > 0:
c_prime -= u
r.append(i)
m = sum([2**k for k in r])
return mAttaques du cryptosystème.
Il existe 3 attaques sur ce chiffrement, nous verrons que certaines existent sous différentes formes avec plusieurs optimisations plus ou moins efficaces.
Pour la suite, voici un code qui génère des Subset Sum Problem en prenant en paramètres :
- La taille de la clé publique (n)
- La densité (d)
(Ce dernier paramètre sera expliqué par la suite)
def gen_example(n, d):
pub = [randint(1, floor(2 ** (n / d))) for _ in range(n)]
assert all(pub.count(x) == 1 for x in pub)
sol = [randint(0, 1) for _ in range(n)]
s = sum(map(lambda x: x[0] * x[1], zip(pub, sol)))
return pub, s, sol- pub contient un sac à dos fort de taille n
- soll contient un message binaire généré aléatoirement de taille n.
- s contient le message chiffré de
sollavec la clépub
Attaque par force brute.
La première attaque est une attaque itérative, elle consiste à tester toutes les possibilités de sous ensemble de la clé publique. Elle est donc fonctionnelle, mais devient rapidement inefficace face à des clés publiques grandes !
Brutefoce naïf
Si on prend un sac à dos de taille n, il y a 2**n possibilités de sous ensembles. En effet, on peut décider pour chaque élément de le conserver ou de le garder ce qui peut être représenté par l’arbre suivant :
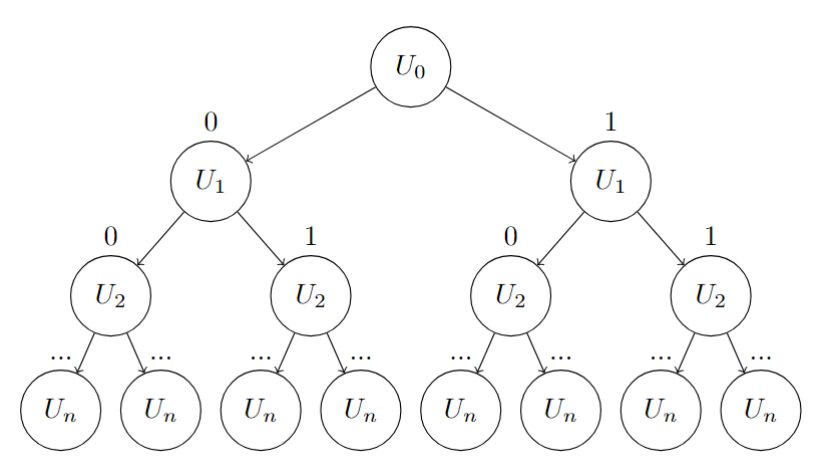
On peut transcrire l’attaque en python :
from itertools import combinations
def solve_bf(pub, s):
size = 1
while size <= len(pub):
for combi in combinations(pub, size):
if sum(combi) == s:
bits = ''.join(['1' if x in combi else '0' for x in pub])
return int(bits, 2)
size += 1
return None
pub, s, sol = gen_example(n=20, d=0.9)
secret = int(''.join([str(x) for x in sol]), 2)
assert solve_bf(pub, s) == secretDiviser pour mieux régner
Une possibilité d’optimisation est de séparer la clé publique en 2 sous ensembles de tailles égales (+/- un élément dans les cas impairs).
On va déterminer toutes les sommes possibles du premier sous-ensemble. Par la suite, on va faire un bruteforce identique sur le second sous ensemble et chercher pour chaque somme possible si la différence manquante pour atteindre le message chiffré existe dans les sommes du premier sous ensemble.
En séparant la clé publique en deux parties et en effectuant des calculs sur ces 2 sous-ensembles, on réduit la complexité par rapport à une approche itérative naïve sur toute la clé publique.
On passe d’une complexité en
O(2^n)à une complexité en
O(2^{n/2})
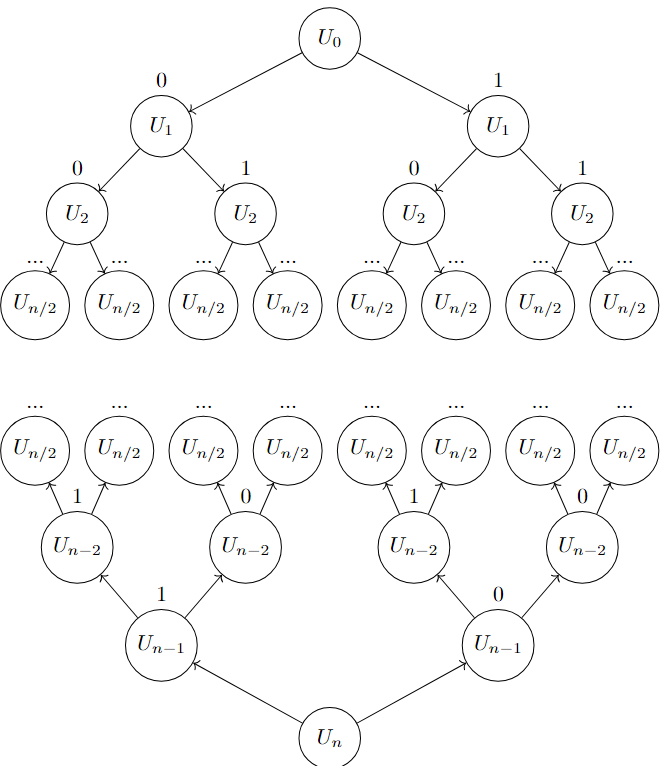
Voici un code python qui effectue cette attaque :
def solve_divideAndConquer(pub, s):
k = len(pub) // 2
pub1, pub2 = pub[:k], pub[k:]
# Bruteforce des sommes du 1er sous-ensemble
r1 = {}
for mask in range(2**k):
x = 0
for i in range(k):
if mask & (1<<i):
x += pub1[i]
r1[x] = mask
# Bruteforce des sommes du 2nd sous-ensemble
for mask in range(2**k):
x = 0
for i in range(k):
if mask & (1<<i):
x += pub2[i]
# Calcul de la différence manquante
target = s - x
# Cherche si la différence manquante a était trouvé dans le 1er sous-ensemble
if target in r1:
m_found = (mask << k) + r1[target]
m_found = int(bin(m_found)[2:].zfill(2*k)[::-1], 2)
return m_found
return None
# Génération d'un exemple de test avec une clé de taille de 60
pub, s, sol = gen_example(n=60, d=0.9)
secret = int(''.join([str(x) for x in sol]), 2)
assert solve_divideAndConquer(pub, s) == secretIl existe d’autres méthodes itératives similaires pour résoudre le Subset Sum Problem avec par exemple l’utilisation de la programmation dynamique.
Ces méthodes fonctionnent, mais sont toutes rapidement limités par la taille de la clé qui fait augmenter le temps de recherche exponentiellement.
Attaques par réseaux Euclidiens.
Avant de se focaliser sur cryptosystème de Merkle-Hellman, une présentation des réseaux euclidiens ainsi que leurs implications dans la cryptographie moderne est nécessaire.
La résolution du Subset Sum Problem peut être faite grâce à l’utilisation de ces outils mathématiques complexes.
Warning: La partie suivante explique brièvement le fonctionnement de concepts mathématiques avancés, la compréhension globale de l’attaque ne requiert pas la compréhension de l’aparté suivante. La conclusion suffit à comprendre le concept dans sa globalité.
Aparté sur les réseaux Euclidiens.
L’étude des réseaux euclidiens en mathématiques remonte au XVIIIe siècle, grâce aux travaux de Leonhard Euler qui a exploré les structures géométriques des points dans l’espace. Cependant, ce n’est qu’au XXe siècle que le concept de réseaux euclidiens a trouvé une application significative en cryptographie.
Dans les années 1990, des chercheurs tels que Ajtai, Dwork, Regev, et d’autres ont introduit les réseaux euclidiens en tant que fondement de problèmes complexes en cryptographie, ouvrant ainsi la voie à de nouvelles avancées dans la construction de systèmes cryptographiques.
Un réseau euclidien ( lattice en anglais) de dimension n est un sous-groupe discret de (R^n, +). C’est une structure géométrique formée par un ensemble de points dans un espace euclidien de dimension finie.
C’est un ensemble discret L de points définis par des combinaisons linéaires entières de vecteurs linéairement indépendants :
L(b_1, b_2, ..., b_n) = \{ \sum_{i=1}^n k_i \times b_i | k_1, k_2, ..., k_n ∈ Z \}On note b la base du réseau :
b = (b_1, b_2,..., b_n)Une image vaut mille mots :
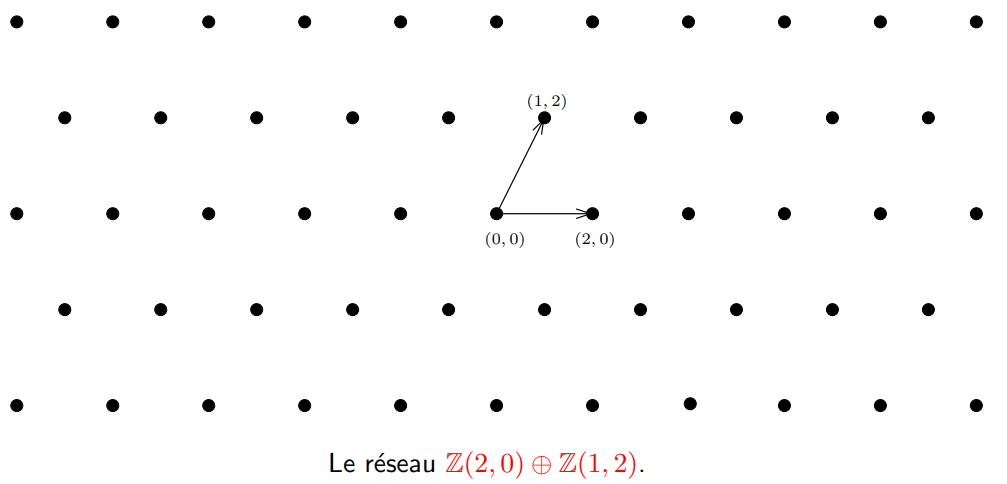
Auteur: David Wong
Ici, on a un réseau euclidien de dimension 2 avec les vecteurs :
\begin{bmatrix} 2 \\\ 0 \end{bmatrix} , \begin{bmatrix} 1 \\\ 2 \end{bmatrix}- On appelle le rang du réseau L, le nombre d’éléments dans une base de L. Ici, nous allons parler des full-rank lattices, ainsi la dimension du réseau sera égale à son rang : m=n.
Ces lattices sont utilisés en cryptographie moderne et introduisent de nouveaux problèmes mathématiques complexes à résoudre.
Parmi eux s’en trouve le CVP
Closest Vector Problem (CVP):
Le Closest Vector Problem (CVP) consiste à trouver le vecteur d’un réseau L le plus proche d’un 2nd vecteur donné dans l’espace euclidien.
Exemple :
- On prend une lattice noté L formée de la base de vecteurs b
- On choisit un vecteur cible noté t
Le CVP consiste à trouver un vecteur v qui minimise la distance euclidienne entre t et v dans la base B
On cherche donc
v \in R^n ~tel~que:~ v = \sum_{i=1}^n v_i \times b_i ~avec~ v_i \in Zet que la distance
|| t-v || = || t - \sum_{i=1}^n v_i \times b_i ||~soit~minimal. 
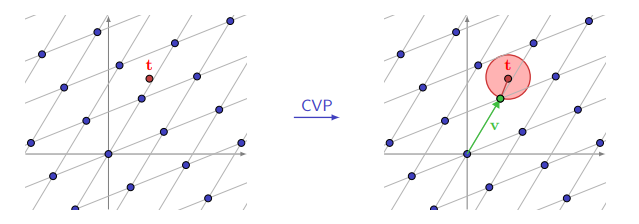
Illustration d’internet
Dans l’exemple ci-dessus, on observe un réseau de dimension 2 avec un vecteur représenté par le point t
La résolution du CVP nous donne le vecteur v qui est le vecteur le plus proche de t dans la base de la lattice.
Résolution du CVP.
L’algorithme de Lenstra, Lenstra et Lovász est une manière de résoudre le CVP.
L’algorithme LLL est une méthode de réduction de base dans un réseau euclidien. Il prend en entrée une base quelconque b et la transforme en une base presque orthogonale, en réduisant la taille des vecteurs.
L’idée principale de l’algorithme LLL est de remplacer les vecteurs de la base qui ne sont pas "presque orthogonaux" par des combinaisons linéaires entières de ces vecteurs. L’algorithme s’exécute en temps polynomial.
Voici un exemple assez visuel :
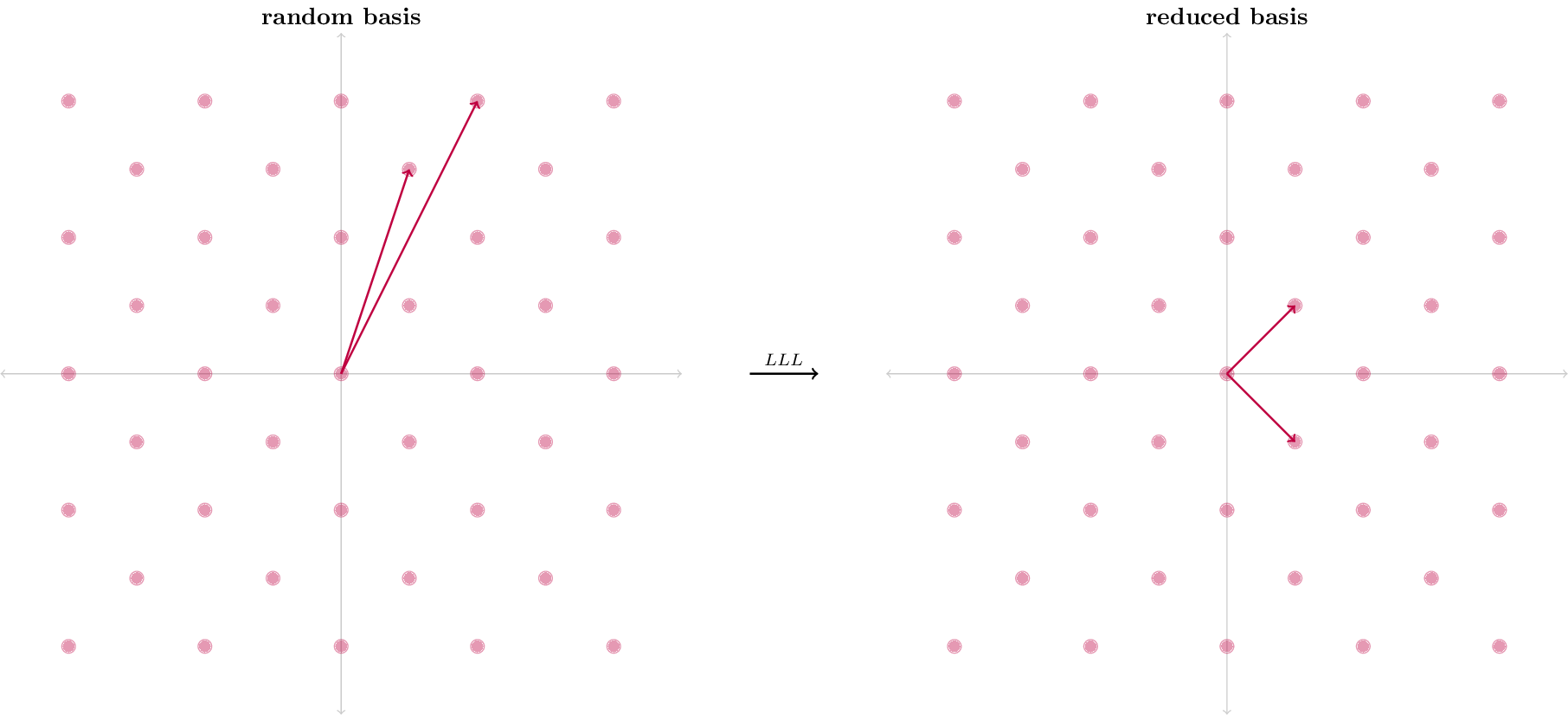
(Auteur : David Wong)
La base de sortie de l’algorithme contient 2 vecteurs plus orthogonaux que la base d’origine.
Exemple :
Voici un exemple de CVP de dimension n que LLL peut résoudre :
On choisit un vecteur secret : S ainsi que des coefficients c_i et on calcule
T = \sum_{i=1}^n s_i*c_iÀ partir de T et C, on cherche à retrouver S.
On peut symboliser l’équation de cette manière :
(s_1, s_2, ..., s_n) \times \begin{pmatrix} c_1 \\ c_2 \\ ... \\ c_n \end{pmatrix} = (T)ou encore :
s_1 \times \begin{pmatrix} c_1 \\ 1 \\ 0 \\ ... \\\ 0 \end{pmatrix} + s_2\times \begin{pmatrix} c_2 \\ 0 \\ 1 \\ ... \\ 0 \end{pmatrix} + … + s_n\times \begin{pmatrix} c_n \\ 0 \\ ... \\ 0 \\ 1\end{pmatrix} = \begin{pmatrix} T \\ s_1 \\ s_2 \\ ... \\ s_n \end{pmatrix}Si on passe la composante T à gauche de l’égalité, on a:
s_1\times \begin{pmatrix} c_1 \\ 1 \\ 0 \\ ... \\\ 0 \end{pmatrix} + s_2\times \begin{pmatrix} c_2 \\ 0 \\ 1 \\ ... \\ 0 \end{pmatrix} + … + s_n\times \begin{pmatrix} c_n \\ 0 \\ ... \\ 0 \\ 1\end{pmatrix} + \begin{pmatrix} -T \\ 0 \\ ... \\ 0 \\ 0\end{pmatrix} = \begin{pmatrix} 0 \\ s_1 \\ s_2 \\ ... \\ s_n \end{pmatrix}Et enfin sous forme matricielle :
(s_1, s_2, ..., s_n, 1) \times \begin{pmatrix} c_1 & 1 & 0 & ... & 0 \\ c_2 & 0 & 1 & ... & 0 \\ ... & ... & ... & ... & 0 \\ c_n & 0 & 0 & ... & 1 \\ -T & 0 & 0 & ... & 0\end{pmatrix} = (0, s_1, s_2, ..., s_n)Une solution du problème est associée à un vecteur court dans le réseau engendré par
(c_1, c_2, ..., c_n, -T)On note :
M = \begin{pmatrix} c_1 & 1 & 0 & ... & 0 \\ c_2 & 0 & 1 & ... & 0 \\ ... & ... & ... & ... & 0 \\ c_n & 0 & 0 & ... & 1 \\ -T & 0 & 0 & ... & 0\end{pmatrix}.En appliquant LLL, la base réduite a de forte chance de contenir un vecteur solution
(0, s_1, s_2, ..., s_n)Code python pour générer un CVP :
from sage.all import *
from random import randint
def gen_problem(size, k=2**50):
S = [randint(1,50) for _ in range(size)]
C = [randint(1,k) for _ in range(size)]
T = sum([xi*ci for xi,ci in zip(S, C)])
return S, C, T
secret, coeff, S = gen_problem(5)
print(S)
print(C)
print(T)Output:
S: [36, 7, 17, 28, 33]
C: [847626201318996, 448733949882171, 1003583485827679, 87764391386129, 1029149080980588]
T: 87135922786900612On peut donc utiliser la bibliothèque SageMath afin de le résoudre :
def solve_cvp(coeff, T):
# Construction de la matrice
A = matrix(ZZ, coeff).T
B = matrix.identity(len(coeff))
C = matrix(ZZ, [-T] + [0 for _ in range(len(coeff))])
M = A.augment(B).stack(C)
# Réduction de la base
B = M.LLL()
# Test des lignes de la matrice de sortie.
for candidate in B.rows():
if candidate[0] == 0:
print(candidate[1:])On construit la matrice M, on applique LLL et on observe les lignes de la matrice résultante:
On a:
M = \begin{pmatrix}
847626201318996 & 1 & 0 & 0 & 0 & 0 \\
448733949882171 & 0 & 1 & 0 & 0 & 0 \\
1003583485827679 & 0 & 0 & 1 & 0 & 0 \\
87764391386129 & 0 & 0 & 0 & 1 & 0 \\
1029149080980588 & 0 & 0 & 0 & 0 & 1 \\
-87135922786900612 & 0 & 0 & 0 & 0 & 0
\end{pmatrix}Après avoir appliqué LLL, on obtient :
B = \begin{pmatrix}
0 & 36 & 7 & 17 & 28 & 33 \\
161 & -146 & -636 & 388 & -111 & 198 \\
734 & 41 & 96 & 312 & 150 & -308 \\
-424 & 188 & -242 & 631 & -31 & -408 \\
-143 & 555 & -287 & -114 & -752 & 182 \\
-444 & 714 & -1553 & -1194 & 1357 & -979
\end{pmatrix}On remarque que le secret S est présent sur la première ligne !
S = (36, 7, 17, 28, 33)Conclusion
Si vous n’avez rien compris au charabia précédent, voici que vous devez retenir :
On utilise les matrices pour représenter des problèmes mathématiques complexes car les mathématiciens ont développé de nombreux outils pour travailler avec.
Parmi ces outils se trouve un algorithme du nom de LLL qui permet de résoudre un problème complexe nommé le CVP.
L’enjeu ici et d’utiliser cet algorithme LLL dans le cas du cryptosystème de Merkle-Hellman en l’adaptant en CVP.
Première attaque: Low Density attack
Vous l’avez peut-être remarqué mais l’exemple précédent sur LLL est très proche de notre système actuel.
Nous sommes en possession :
- D’une somme (Message chiffré) noté C
- D’un ensemble de coefficients (Clé publique) noté U
et nous cherchons un secret (m) composé de 0 et de 1 correspondant au secret de l’exemple précédent.
Lagarias et Odlyzko présentent en mai 1977 une méthode (LO Method) pour casser le Subset Sum Problem, ils proposent d’appliquer LLL à la matrice suivante :
M = \begin{pmatrix} 1 & 0 & ... & 0 & N*U_1 \\ 0 & 1 & ... & 0 & N*U_2\\ ... & ... & ... & ... & ...\\ 0 & 0 & ... & 1 & N*U_n \\ 0 & 0 & ... & 0 & -N*C\end{pmatrix}avec N un coefficient dépendant de la taille de la clé publique :
N=\lceil n^{1/2} \rceil +1De la même manière que le CVP de l’exemple précédent, on retrouve le vecteur :
(m_1,m_2,..., m_n,0)contenant les bits du secret m.
En python:
def solver_lattice_lo(pub: list[int], s: int, secret: int, N:int):
# Création de la matrice
M = matrix.identity(len(pub))
M = M.augment(N * matrix(ZZ, pub).T)
M = M.stack(matrix(ZZ, [0 for _ in range(len(pub))] + [N * s]))
# LLL
B = M.LLL()
# Vérification de toute les lignes
candidates = [Y for Y in B if abs(Y[-1]) == 0]
for C in candidates:
# On peut trouver (m_1,m_2,..., m_n,0) ou (-m_1,-m_2,...,-m_n,0)
for k in [-1,1]:
C2 = (k * vector(C))[:-1] # On supprime la dernière composante du vecteur solution (0)
# Vérification que la ligne contient uniquement des 0 et des 1
if all([x in [0, 1] for x in C2]):
# Vérification de la solution trouvée
secret_ = int(''.join([str(x) for x in C2]), 2)
if secret_ == secret:
return True
return False
pub, C, sol = gen_example(n=50, 0.4)
secret = int(''.join([str(x) for x in sol]), 2)
N = ceil(len(pub)**0.5)
assert solver_lattice_lo(pub, C, secret, N)Performances :
Cette méthode est très efficace et presque instantanée comparé au bruteforce. En revanche, celle-ci présente plusieurs faiblesses.
Les taux de réussite de la résolution dépendent de deux paramètres :
- La dimension de la matrice
- La densité du problème qu’on cherche à résoudre.
Le premier paramètre est assez intuitif : plus il y a d’inconnus, plus la matrice est grande et moins LLL est efficace. La dimension de la matrice est ici égale à la taille de la clé publique + 1. Ainsi, plus la clé sera longue et moins, il sera facile de casser le knapsack.
Le 2nd paramètre est moins évident, LLL, l’algorithme miracle qui nous permet de trouver une solution au CVP est plus efficace quand les différences entre les coefficients connus et les coefficients cherchés sont grandes.
En effet, plus la taille des nombres composants la clé publique est grande, plus l’algorithme est performant.
C’est ainsi qu’on définit la notion de densité du problème :
\lambda = n / \log_2(max(U_i))La densité λ est donc un indice compris entre 0 et 1 qui quantifie la facilité de résolution du Subset Sum Problem.
Lagarias et Odlyzko ont montré que leur technique fonctionnait avec des problèmes dont les densités étaient inférieures à 0.6463
Améliorations
Première amélioration :
Il existe un algorithme plus performant que LLL: BKZ est une généralisation de LLL plus efficace et plus récente.
BKZ est aussi un algorithme de réduction sur des matrices, mais celui prend en plus un paramètre β représentant une taille de bloc utilisé dans l’algorithme.
Plus ce paramètre β est grand et plus les résultats seront précis.En revanche, le temps de calcul sera plus long.
LLL est un cas particulier de BKZ avec une taille de bloc égale à 2.
Seconde amélioration :
En 1992 Coster, Joux, LaMacchia, Odlyzko, Schnorr et Stern ont démontré qu’il était possible de repousser cette densité maximale de $0.6463$ à $0.9408$ ! (CJLOSS Method)
En effet, grâce à deux optimisations majeures sur la matrice de base, l’efficacité de l’attaque par faible densité a grandement augmenté !
- Le premier changement dans leur lattice et de remplacer le dernier vecteur de la matrice M en remplaçant les 0 par des -½ :
M = \begin{pmatrix} 1 & 0 & ... & 0 & N*U_1 \\ 0 & 1 & ... & 0 & N*U_2\\ ... & ... & ... & ... & ...\\ 0 & 0 & ... & 1 & N*U_n \\ -\frac{1}{2} & -\frac{1}{2} & ... & -\frac{1}{2} & -N*C\end{pmatrix}Ce qui mène donc à l’équation suivante :
\begin{pmatrix}
m_1 \\
m_2 \\
... \\
m_n \\
1 \\
\end{pmatrix} ^T \times \begin{pmatrix} 1 & 0 & ... & 0 & N*U_1 \\ 0 & 1 & ... & 0 & N*U_2\\ ... & ... & ... & ... & ...\\ 0 & 0 & ... & 1 & N*U_n \\ -\frac{1}{2} & -\frac{1}{2} & ... & -\frac{1}{2} & -N*C\end{pmatrix}
=
\begin{pmatrix}
m_1-\frac{1}{2} \\
m_2-\frac{1}{2} \\
... \\
m_n-\frac{1}{2} \\
0 \\
\end{pmatrix} ^TEn appliquant LLL sur cette nouvelle matrice M, le vecteur retrouvé sera
(m_1-\frac{1}{2}, m_2-\frac{1}{2}, ..., m_n-\frac{1}{2}, 0)Il suffira d’ajouter ½ aux n-premières composantes pour retrouver le message d’origine m.
Ce changement augmente grandement l’efficacité de LLL car il va chercher à trouver le plus petit vecteur dans la base donnée. Il va donc être plus efficace si le vecteur visé est plus proche du vecteur nul.
- Le second changement est la valeur du coefficient N qui est maintenant à
N=\lceil \frac{n^{1/2}}{2} \rceil +1
Enfin, une dernière optimisation existe en multipliant par des coefficients K=K’=2 certaines parties de la matrice :
M = \begin{pmatrix}
K' & 0 & ... & 0 & K' \times N \times U_1 \\
0 & K' & ... & 0 & K' \times N \times U_2\\
... & ... & ... & ... & ...\\
0 & 0 & ... & K' & K' \times N \times U_n \\
-K \times \frac{1}{2} & -K \times \frac{1}{2} & ... & -K \times \frac{1}{2} & -K' \times N \times C\end{pmatrix}
= \begin{pmatrix}
2 & 0 & ... & 0 & 2\times N \times U_1 \\
0 & 2 & ... & 0 & 2 \times N \times U_2\\
... & ... & ... & ... & ...\\ 0 & 0 & ... & 2 & 2 \times N \times U_n \\
-1 & -1 & ... & -1 & -2 \times N \times C
\end{pmatrix}Comparaisons
Toutes ces différentes modifications ont été reprises afin d’en faire des combinaisons et de voir quelles optimisations étaient les plus efficaces.
Voici donc les différents paramètres testés:
- Algorithme de réductions : BKZ ou LLL
- Absence ou présence des coefficients non nul sur le dernier vecteur
- Valeurs de N possibles :
N \in ( \lceil n^{1/2} \rceil +1, \lceil \frac{n^{½}}{2} \rceil +1) - Valeurs de K possibles: 1, 2
- Valeurs de K’ possibles: 1, 2
Pour chaque cas possible, 40 Subset Sum Problem de taille n=20, 45 et enfin 60 ont été générés avec des densités allant de 0.5 à 1
Il y a eu 11
Sur les résultats, on confirme tout de suite que plus la taille du problème est grande, plus LLL à du mal à trouver une solution, qu’importe les méthodes et lattices utilisés.
Voici les résultats pour n=45:
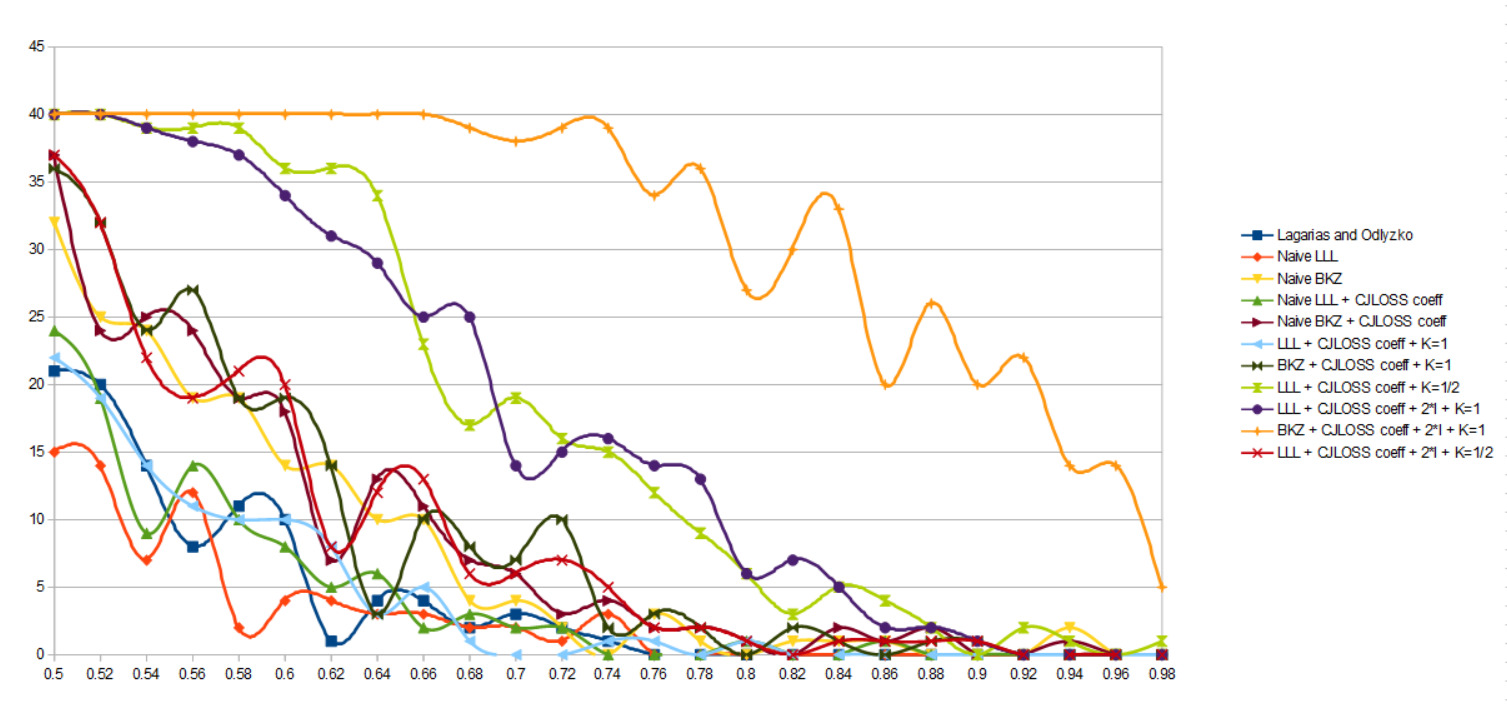
On retrouve des résultats en accord avec les optimisations présentées. La méthode CJLOSS est plus efficace que LO.
La méthode LO fonctionne une fois sur deux pour des densités faibles alors que CJLOSS fonctionne à 100% jusqu’à une densité de λ=0.66 environ.
L’optimisation la plus efficace est ici :
- Algorithme : BKZ
- K = 2
- K’= 2
- N = ⌈2**½/2⌉+1
Ce qui forme la matrice suivante :
M = \begin{pmatrix}
2 & 0 & ... & 0 & 2 \times (\lceil \frac{n^{1/2}}{2} \rceil +1) \times U_1 \\
0 & 2 & ... & 0 & 2 \times (\lceil \frac{n^{1/2}}{2} \rceil +1) \times U_2\\
... & ... & ... & ... & ...\\
0 & 0 & ... & 2 & 2 \times (\lceil \frac{n^{1/2}}{2} \rceil +1) \times U_n \\
-1 & -1 & ... & -1 & -2 \times (\lceil \frac{n^{1/2}}{2} \rceil +1) \times C
\end{pmatrix}Des résultats similaires sont observés pour n=20 :
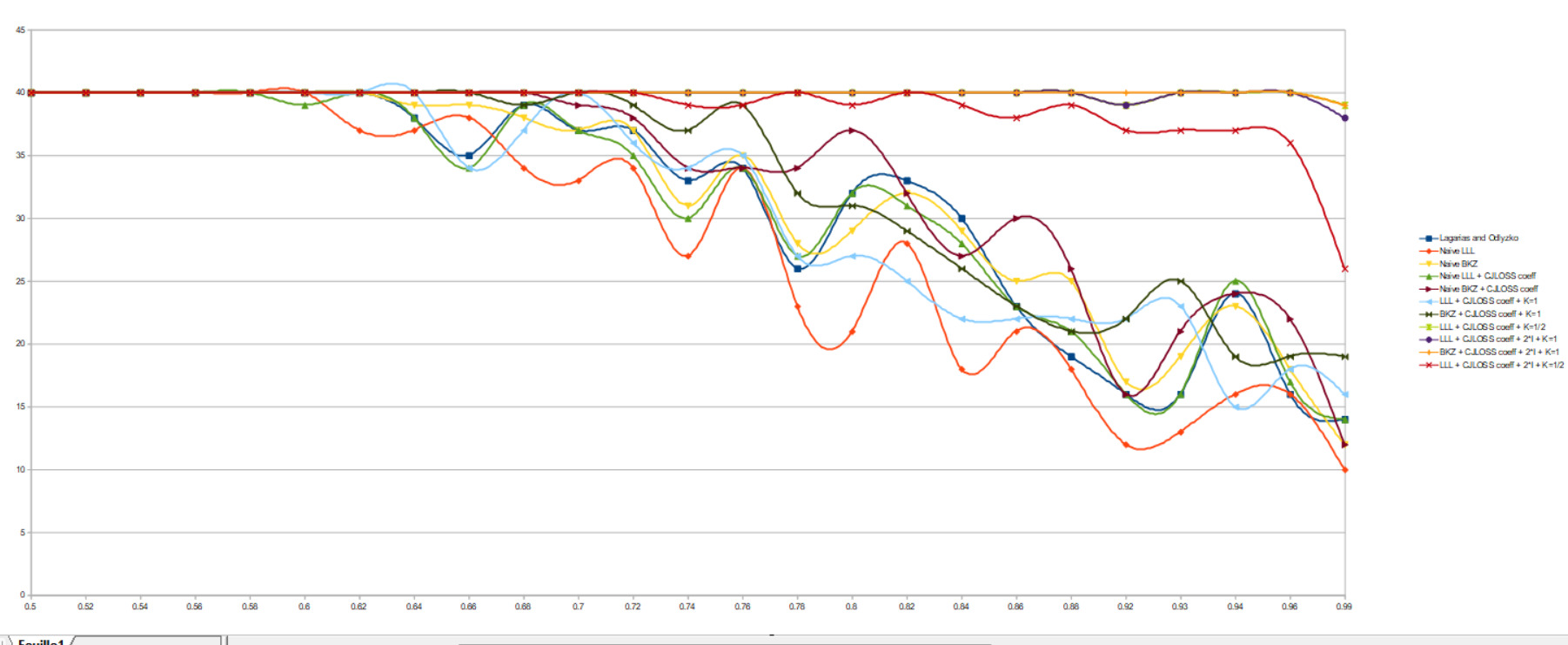
Voici le code python complet en utilisant la matrice M:
def solver_knapsack(pub: list[int], s: int, secret: int):
# Calcul de N
N = ceil(len(pub)**0.5 / 2) + 1
# Création de la matrice
M = 2 * matrix.identity(len(pub))
M = M.augment(2 * N * matrix(ZZ, pub).transpose())
M = M.stack(-1 * matrix(ZZ, [1 for _ in range(len(pub))] + [2 * N * s] ))
# Réduction
B = M.BKZ()
# Récupération des candidats potentiels.
candidates = [Y for Y in B if abs(Y[-1]) == 0]
for C in candidates:
for k in [-1,1]:
# Récupération des m_i
C2 = [(-x+2)//2 for x in (k * vector(C))[:-1]]
# Vérification de la solution trouvé.
if all([x in [0, 1] for x in C2]):
secret_ = int(''.join([str(int(x)) for x in C2]), 2)
if secret_ == secret:
return True
return False
pub, C, sol = gen_example(n=50, d=0.8)
secret = int(''.join([str(x) for x in sol]), 2)
assert solver_knapsack(pub, C, secret)Seconde attaque : Shamir attack
Cette dernière attaque est la plus ancienne et l’une des moins efficaces mais elle reste cependant très intéressante.
On rappelle les notations et relations suivantes :
Une clé publique :
U = (u_1, u_2, ...,u_n)et une clé privée :
B = (b_1, b_2, ...,b_n)avec
\forall i \in [1,n]~;~b_i = u_i \times w \mod ACe qui veut dire que :
\forall i \in [1,n]~; ∃ k_i \in Z ;~b_i = u_i \times w -k_i AAinsi, on a :
\frac{w}{A} - \frac{k_i}{u_i} = \frac{b_i}{k_i\times A}ce qui implique que les
\frac{k_i}{u_i}sont proches de
\frac{w}{A}De plus, les b_i forment une séquence super-croissante donc :
b_i < \frac{A}{2^{n-i}}ou
\frac{w}{A} - \frac{k_1}{u_1} < \frac{1}{a_1 \times 2^{n-1}}est très petit.
*Shamir s’est rendu compte qu’il suffisait de trouver une paire (a, m) tel que les au_i % m forment une séquence super-croissante pour casser le knapsack.**
Shamir démontre que :
|u_i \times k_1-u_1 \times k_i| = |u_1 \times b_i-u_i \times b_1 | < 2 \times b_iet qu’ainsi :
- a = k1
- m=u1
sont de bons candidats.
La dernière étape dans le raisonnement de Shamir est de trouver k1, il reformule l’équation précédente sous forme matricielle avec
0 < \lambda <1 et
1 < l \leq n(k_1, k_2, ..., k_l) \times \begin{pmatrix}
\lambda & u_2 & u_3 & ... & u_l \\
0 & -u_1 & 0 & ... & 0 \\
0 & 0 & -u_1 & ... & 0 \\
... & ... & ... & ... & ... \\
0 & 0 & 0 & ... & -u_1
\end{pmatrix} = (\lambda \times k_1, k_1 \times u_2-k_2 \times u1, ...,k_1 \times u_l-k_l \times u_1)On définit
\lambda = 2^{x+1}avec x le nombre maximal de bit des u_i
Le vecteur de droite étant petit (Voir minoration dans l’égalité précédente), les algorithmes de réduction de base présentés plus haut vont pouvoir le retrouver aisément.
Il pose donc M la lattice suivante :
M = \begin{pmatrix} \lambda & u_2 & u_3 & ... & u_l \\ 0 & -u_1 & 0 & ... & 0 \\ 0 & 0 & -u_1 & ... & 0 \\ ... & ... & ... & ... & ... \\ 0 & 0 & 0 & ... & -u_1 \end{pmatrix}En appliquant LLL sur M, on obtient le vecteur solution contenant k_1
En posant (a, m)=(k_1, a_1) , on peut recalculer une nouvelle clé privée b’ permettant le déchiffrement de n’importe quel message.
b_i' = a*u_i \mod m = k_1*u_i \mod a_iPour n’importe quel message C, l’attaquant calcule C’
C'=a* C \mod n = k_1 * C \mod nIl peut ainsi déchiffrer C en décomposant C’ avec la nouvelle clé privée b.
Une petite subtilité est que le premier bit du message déchiffré ne peut être retrouvé et doit donc être bruteforce.
Exemple
On reprend les valeurs fournies par la publication de Shamir:
U = [2021, 929, 2278, 1863, 1285, 302, 105, 294]C = 5983m = 171On forme la matrice M suivante :
M = \begin{pmatrix} \frac{1}{2^5} & 929 & 2278 &1863 \\ 0 & -2021 & 0 & 0 \\ 0 & 0 & -2021 & 0 \\ 0 & 0 & 0 & -2021 \end{pmatrix}On obtient après LLL
B = \begin{pmatrix} \frac{409}{32} & 13 & 21 & 50 \\~\\ \frac{2021}{32} & 0 & 0 & 0 \\~\\ \frac{-755}{32} & -108 & -19 & 51 \\ ~\\\frac{205}{8} & -137 & 556 & -216 \end{pmatrix}On a donc :
- u = k_1 = 409
- m = a_1 = 2021
On calcule la nouvelle clé privée :
b'= \{0, 13, 21, 50, 105, 237, 504, 1007\} Puis
C'= 5983*409 \mod 2021 = 1637Enfin, on décompose C’ :
1637 = 1007 + 504 + 105 + 21ce qui correspond au binaire : 0101011
Il y a donc 2 possibilités :
0010101110101011
Voici un code python pour cette attaque :
from sage.all import *
def solver_shamir(pub, s, secret, l=4):
# Calcul de λ
λ = 1 / (2 ** (ceil(log(int(max(pub)).bit_length(), 2))+1))
# Création de la *lattice* M
ui = pub[:l]
A = matrix(QQ, [λ] + ui[1:])
B = matrix.diagonal([-ui[0] for _ in range(l-1)])
C = matrix(QQ, [0 for _ in range(l-1)]).transpose()
M = A.stack(C.augment(B))
# Réduction de M
B = M.LLL()
# m = u1
m = ui[0]
# Récupération des k1 possibles.
for r in B.rows():
# a = k1
a = k1 = abs(r[0].numerator())
# Calcul de la clé privée b'
priv = [(a * ui) % m for ui in pub]
c_prime = (s * a) % m
if c_prime == 0:
continue
# Déchiffrement avec b'
r1 = ''
for i, x in enumerate(priv[::-1][:-1]):
if c_prime >= x and x > 0:
c_prime -= x
r1 += '1'
else:
r1 += '0'
if c_prime == 0:
# Bruteforce du MSB
for x1 in [1, 0]:
r2 = r1 + str(x1)
m_found = int(r2[::-1], 2)
if m_found == secret:
return True
return False
# Exemple extrait de la publication de Shamir
pub = [2021, 929, 2278, 1863, 1285, 302, 105, 294]
s = 5983
secret = 171
assert solver_shamir(pub, s, secret, l=4)
# Exemple généré aléatoirement
pub, s, sol = gen_example(n=10, d=0.5)
secret = int(''.join([str(x) for x in sol]), 2)
assert solver_shamir(pub, s, secret, l=5)Conclusion
Après l’introduction de l'algorithme LLL, des ajustements ont été opérés sur le schéma knapsack afin d’en renforcer la sécurité. Parallèlement, l’algorithme LLL, notamment dans sa version élaborée par Schnorr, a évolué avec le système knapsack.
C’est Shamir qui a été le premier dans l’application de l'algorithme LLL pour compromettre le cryptosystème Merkle-Hellman, en utilisant l’algorithme de programmation linéaire de Lenstra. Des améliorations ultérieures ont été apportées, conduisant à la compromission de tous les systèmes de clés publiques à sacs à trappes connus.
Références :
- Improved low-density subset sum algorithms (Matthijs J. Coster, Antoine Joux, Brian A. LaMacchia, Andrew M. Odlyzko, Claus-Peter Schnorr, Jacques Stern)
- Low-Density Attack Revisited (Tetsuya Izu, Jun Kogure, Takeshi Koshiba, Takeshi Shimoyama)
- Cryptanalysis of two knapsack public-key cryptosystem (Jingguo, Xianmeng Meng, Lidong Han)
- “Mathematics of Public Key Cryptography" 2.0 Chapter 19 (Steven Galbraith)
- On the Lagarias-Odlyzsko algorithm for the subset sum problem (A. M. Frieze)
- Lattices and Tikz (David Wong)
- CTF Writeup (Tsumiiiiiiii)
- CTF Writeup (Connor McCartney)
- Crypto.stackexchange post
- Wikipedia
- The Knapsack Problem and the LLL Algorithm (Jennifer Bakker)
- BKZ 2.0: Better Lattice Security Estimates (Yuanmi Chen , Phong Q. Nguyen)
- Lattice Blog Reduction – Part I: BKZ (Michael Walter)
- A Polynomial-Time Algorithm for Solving the Hidden Subset Sum Problem (Jean-Sébastien Coron and Agnese Gini)
Auteur
Article écrit par Arthur Deloffre alias Vozec, alternant en Test d’Intrusion chez ACCEIS.