À l’occasion du salon leHack 2024, un challenge sur les courbes elliptiques a été proposé lors du CTF. Cet article va présenter les différentes pistes que j’ai explorées lors de la compétition puis une méthode de résolution de ce challenge. Ce challenge est le seul qui n’a pas été résolu lors de la compétition.

Découverte du challenge

Ce challenge est proposé par JosePisco, étudiant à Epita et se base sur un problème mathématique très connu, le ECDLP.

Voici le code source :

from Crypto.Hash import SHA1
from Crypto.Random.random import randint
from Crypto.Util.number import bytes_to_long, isPrime
from sage.all import *
from secret import FLAG
import os

def beep_boop_error(err):
    print("Beep boop! Error you are not an admin! " + err)

def try_building_curve(a, b, p):
    if not isPrime(p) or int(p).bit_length() < 160:
        beep_boop_error("My admins use big primes for their curves!")
        return False
    try:
        E = EllipticCurve(GF(p), [a, b])
    except:
        beep_boop_error("My admins use elliptic curves!!")
        return False

    n = E.order()
    if factor(n)[-1][0] < 2^128 or n == p:
        beep_boop_error("My admins use safe curves!!!")
        return False

    for k in range(1, 13):
        if (p^k - 1) % n == 0:
            beep_boop_error("Curve embedding degree is too small!!!!")
            return False

    return E

class Challenge:
    def __init__(self):
        self.msg = b'leHack2024 admin portal' + os.urandom(16)
        print("To authenticate yourself as my admin, you must sign this message:", self.msg.hex())
        print()

    def verify(self, r, s):
        h = bytes_to_long(SHA1.new(self.msg).digest())

        s_inv = Integer(pow(s, -1, self.order))
        R = (h * s_inv) * self.G + (r * s_inv) * self.P
        return R[0] == r

    def run(self):
        print("Imagine losing your x509? Just kidding... unless?")
        print("Give me elliptic curves parameters:")
        p = int(input("p = "))
        a = int(input("a = "))
        b = int(input("b = "))

        E = try_building_curve(a, b, p)
        if E is False:
            return

        self.E = E
        self.order = self.E.order()

        self.G = E.gens()[0]
        self.__d = randint(2, p - 1)
        self.P = self.__d * self.G

        print("Here is the admin's public key:", self.P)

        r = Integer(input("r = "))
        s = Integer(input("s = "))

        if self.verify(r, s):
            print(FLAG)
        else:
            beep_boop_error("INCORRECT SIGNATURE, INTRUDER DETECTED! BEEP BOOP!!!!")

if __name__ == "__main__":
    chall = Challenge()
    chall.run()

Le serveur nous demande de lui fournir trois paramètres afin de définir une courbe elliptique. À partir de cette courbe, il génère une paire de clé privée / publique, nous transmet la clé publique et nous demande de signer un message aléatoire.
En fonction de la validité de cette signature, il nous renvoie une erreur ou le flag.

Ce serveur implémente un système de signature sur les courbes elliptiques appelé ECDSA.
Ce système réside sur un problème mathématique appelé le ECDLP, un logarithme discret sur des courbes elliptiques.

Afin de mieux comprendre ce problème, voici un résumé sur ses objets mathématiques puis une explication du problème mathématique.

Rappels sur les courbes elliptiques

Les courbes elliptiques sont des objets mathématiques avec des applications importantes en cryptographie, en théorie des nombres et dans de nombreux autres domaines de la mathématique.

Une courbe elliptique est un ensemble de points (x, y) qui satisfont une équation de la forme :

 $y^2 = x^3 + ax + b$

où a et b sont des coefficients qui déterminent la forme spécifique de la courbe. Cette équation est souvent appelée l’équation de Weierstrass.

Pour que l’ensemble des solutions forme une courbe elliptique au sens strict, il est nécessaire que le discriminant de l’équation, donné par :

 $\Delta=-16*(4*a^3)+27*b^2$

soit non nul.
Cette condition assure que la courbe n’a pas de points singuliers, c’est-à-dire de cusps ou de croisements.

Voici un exemple de plusieurs courbes elliptiques :

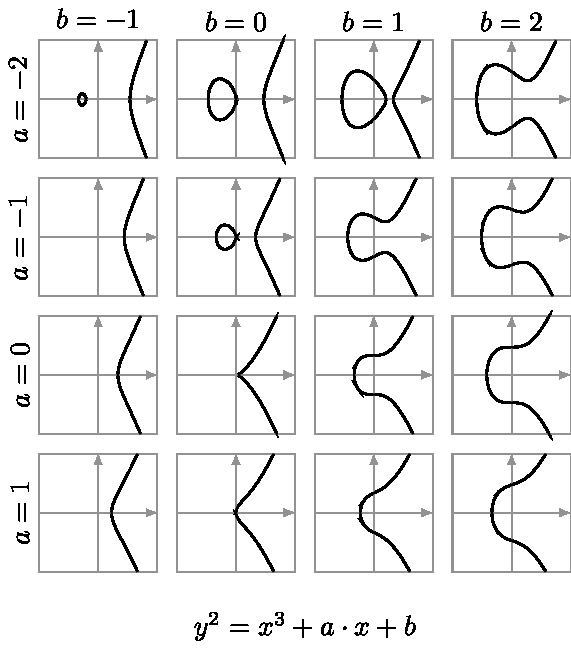
Points à l’infini

En plus des points sur le plan, les courbes elliptiques incluent également un point à l’infini, noté

$O$

qui sert d’élément neutre pour l’addition de points sur la courbe.

Addition des points

L’addition de deux points sur une courbe elliptique est définie géométriquement. Pour additionner deux points P et Q on procède de la manière suivante :

Tracer une ligne droite passant par P et Q
Cette ligne coupera la courbe en un troisième point R’
Le point R, qui est l’addition P+Q est le reflet de R’ par rapport à l’axe des abscisses

Cas particuliers

Addition d’un point à lui-même (doublage)
Pour doubler un point P = (x, y), on utilise la formule suivante pour trouver 2*P :

 $s = \frac{3x^2 + a}{2y} \newline x_{2P} = s^2 - 2x \newline y_{2P} = s(x - x_{2P}) - y$

Addition avec le point à l’infini:
Pour tout point P:

 $P + \mathcal{O} = \mathcal{O} + P = P$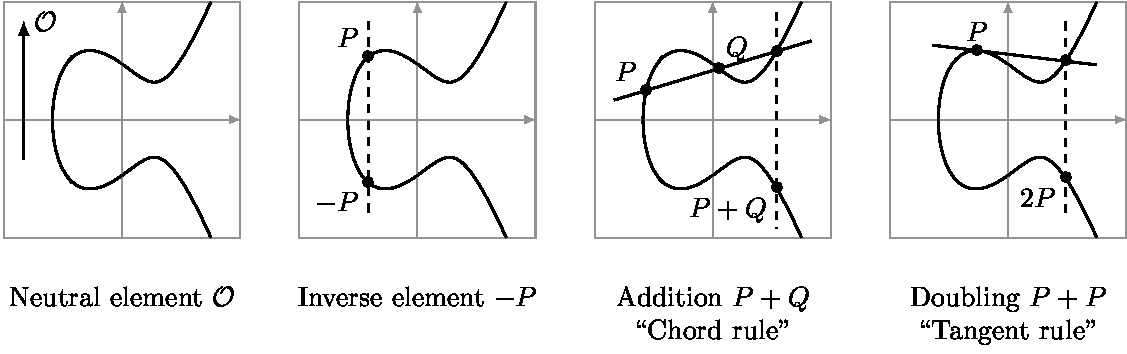

Multiplication des points

La multiplication d’un point P par un entier n est simplement l’addition de
P à lui-même n fois.
Cette opération peut être effectuée efficacement en utilisant l’algorithme de doublement et addition, aussi connu sous le nom de "méthode des doubles et des ajouts".

Le Problème du Logarithme Discret sur les Courbes Elliptiques (ECC)

Le problème du logarithme discret elliptique (ECDLP) est l’analogue du problème du logarithme discret dans les courbes elliptiques, similaire à celui rencontré dans d’autres groupes algébriques comme les groupes multiplicatifs des corps finis.

Définition du problème

Sur une courbe elliptique, le problème du logarithme discret peut être formulé comme suit : étant donné deux points P et Q sur une courbe elliptique, trouver un entier k tel que :

 $Q = k*P$

où k est le "logarithme" de Q à la base P.
En d’autres termes, k est le facteur de multiplication scalaire qui, lorsqu’il est appliqué à P, produit Q.

Difficulté du problème

La sécurité de nombreux systèmes de cryptographie basés sur les courbes elliptiques, repose sur la difficulté de résoudre ce problème du logarithme discret.

Comparé à son équivalent dans les groupes multiplicatifs des corps finis, le problème du logarithme discret sur les courbes elliptiques est généralement plus difficile à résoudre pour des tailles de clé équivalentes.

Cela permet d’utiliser des clés plus courtes tout en maintenant un niveau de sécurité comparable, ce qui se traduit par des gains en termes d’efficacité et de performance.

Fonctionnement de l’ECDSA (Elliptic Curve Digital Signature Algorithm)

L’ECDSA (Elliptic Curve Digital Signature Algorithm) est une variante de l’algorithme de signature numérique DSA qui utilise les propriétés des courbes elliptiques pour améliorer la sécurité et l’efficacité. Voici comment il fonctionne, étape par étape.

1. Prérequis

Pour utiliser l’ECDSA, il est nécessaire de disposer :

D’une courbe elliptique E sur un corps fini Fp
D’un point de base G sur E, dont l’ordre (nombre de multiple de G avant de retomber sur le point à l’infini) est un grand nombre premier n.

2. Génération des clés

Clé privée : Le signataire choisit un nombre aléatoire d compris entre 1 et n−1. Ce nombre d sert de clé privée.
Clé publique : La clé publique Qest calculée en multipliant le point de base G par la clé privée *d:

 $Q = d*G$

3. Signature d’un message

Pour signer un message m, le signataire procède comme suit :

Hachage du message: Calculer le hachage H(m) du message à signer m, ou H est une fonction de hachage cryptographique tel que la famille des shaX. Ce hash est ensuite réduit modulo n pour obtenir z.
Génération d’un nombre aléatoire : Choisir un nombre aléatoire k entre 1 et n-1
Calcul de coordonnées du point : Calculer le point k*G=(x1, y1) et appliquer le modulo n à x1 afin d’obtenir r. (Si r=0, choisir un autre k et recommencer.)
Calcul de la signature : On calcule

 $s = k^{-1}*(z + rd) \pmod{n}$

(Si s=0, on recommence avec une autre valeur de *k*)

Pour résumer, on a :

 $k = random(1, n-1) \newline z = H(m) \pmod{n} \newline r = (k * G).x \pmod{n} \newline s = k^{-1}*(z + r*d) \pmod{n}$

La signature est le couple (r, s)

4. Vérification de la Signature

Pour vérifier la signature (r, s) d’un message m avec la clé publique Q, on effectue les étapes suivantes :

Vérifier les paramètres : S’assurer que r et s sont compris entre 1 et n-1
Hachage du message : On calcule le hash de m:

 $z = H(m) \pmod{n}$

Calcule de l’inverse de s:
```
 $w = s^{-1} \pmod{n}$ 
```

Calculer u1 et u2:

 $u_1 = z*w \pmod{n} \newline u_2 = r*w \pmod{n}$

Calculer le point X:
```
 $X = u_1*G + u_2*Q$ 
```
(Si X est le point à l’infini, alors la signature est invalide.)
Calculer v : La coordonnée x de X modulo n donne v.
Si v = r, la signature est valide. Sinon, elle est invalide.

Application à notre challenge.

Nous devons fournir au serveur une courbe elliptique puis résoudre le logarithme discret sur cette même courbe. Toute la difficulté du challenge réside donc dans le fait de trouver une courbe dont il est facile de résoudre ce problème.

Il sera ainsi facile de retrouver la clé privée d à partir de sa base G et de la clé privée Q:

 $Q = d*G$

Une fois la clé privée d retrouvée, il sera ainsi possible de signer n’importe quel message.

Analyse de la fonction try_building_curve

Première vérification

Nos paramètres a, b et p sont passés à une fonction try_building_curve qui crée la courbe et effectue plusieurs tests afin de vérifier sa robustesse, nous allons les détailler un à un.

La première vérification est la primalité de p.
En effet, grâce à la librairie pycryptodome il vérifie que p est premier et qu’il est supérieur à 2160.

Il s’assure ici qu’il n’est pas possible de résoudre le logarithme discret facilement grâce à l’utilisation d’une petite courbe.

Seconde vérification

Il définit ici la courbe noté E:

try:
    E = EllipticCurve(GF(p), [a, b])
except:
    beep_boop_error("My admins use elliptic curves!!")
    return False

Il empêche de manière implicite l’utilisation de courbe singular.
Si on reprend la définition des courbes elliptiques décrite précédemment, on note que

 $\Delta=-16*(4*a^3)+27*b^2$

doit être différent de 0.
Si on choisit spécifiquement a et b afin que Δ soit égal à 0, on définit une courbe dite "singular"

Dans ce cas-là, il existe 2 ou 3 points singuliers sur la courbe.

Exemple de point singulier en (0, 0.5)

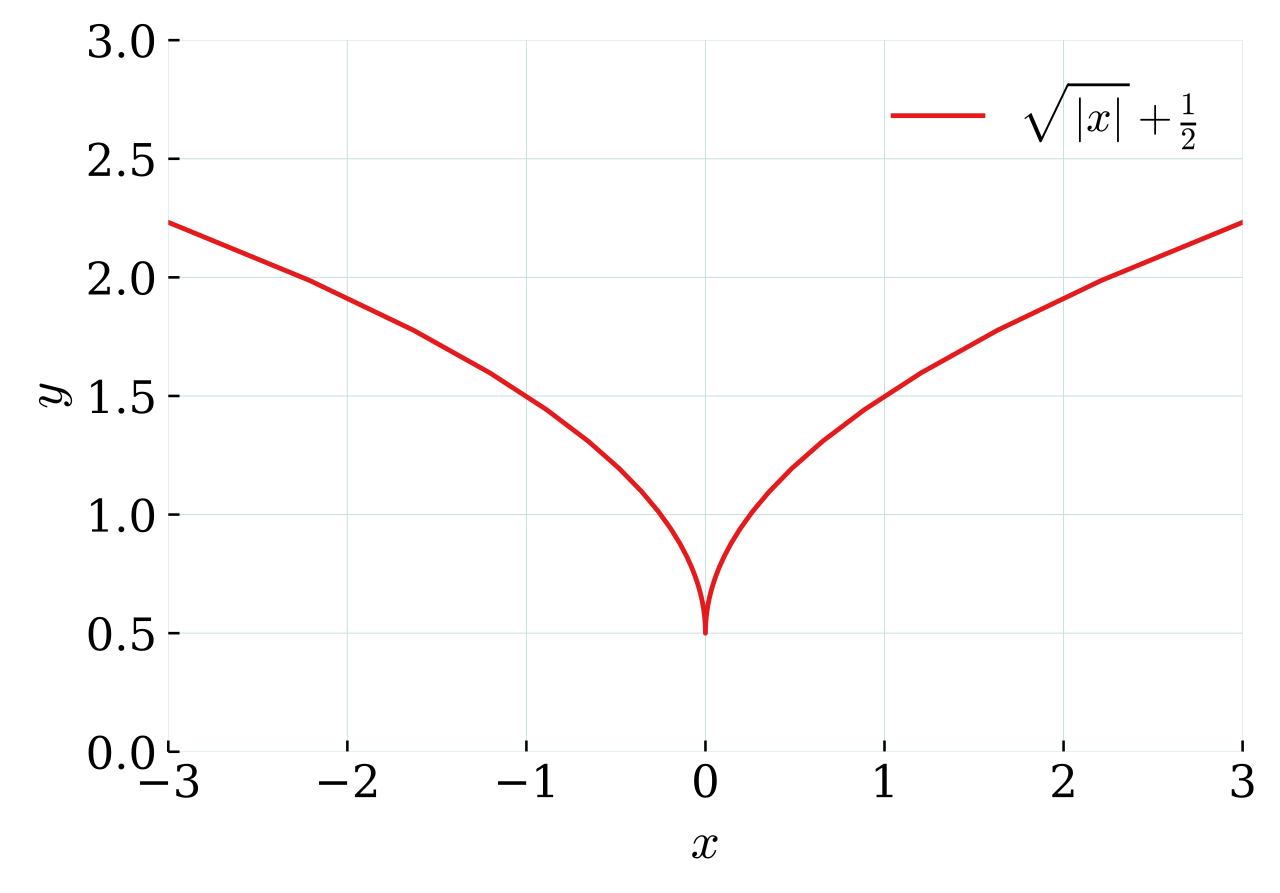
Dans ce cas-là, on faisait des changements de variables, on peut changer la courbe en :

 $y^2 = x^3$

 $y^2 = x^2 * (x-1)$

Dans le premier cas, la courbe est isomorphique au groupe additif Fp
Dans le second cas, la courbe est isomorphique au groupe additif Fp2*

Dans ces deux cas, le logarithme discret est trivial à résoudre dans les groupes associés. Il est ainsi aisé de le résoudre puis d’utiliser la propriété isomorphique pour retrouver la solution sur la courbe d’origine.

Malheuresement, sagemath déclenche une erreur lors de la création de telle courbe et le serveur ferme la connexion TCP :

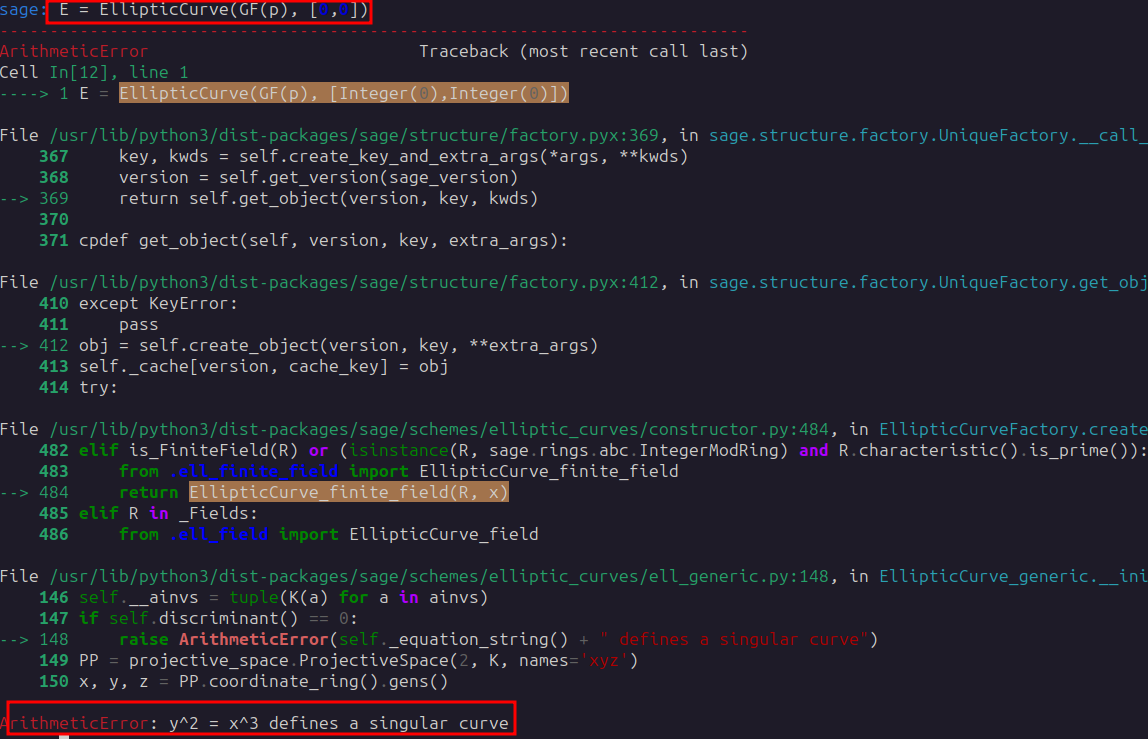
Troisième vérification :

Par la suite, le serveur exécute ce code :

n = E.order()
if factor(n)[-1][0] < 2^128:
    beep_boop_error("My admins use safe curves!!!")
        return False

Il vérifie que le plus grand facteur de l’ordre de la courbe soit supérieur à 2^128.

Cette vérification empêche l’attaque de Pohlig-Hellman sur la courbe.
(La clé privée est correctement générée entre 1 et n-1)

Pohlig-Hellman est un algorithme permettant de résoudre le logarithme discret sur tous les sous groupes puis de combiner les différentes petites solutions grâce au théorème des restes chinois afin de trouver une solution générale.

Cet algorithme permet donc de réduire la complexité du logarithme discret en passant d’un problème sur un groupe d’ordre n à un sous-groupe de la taille du plus grands facteurs de n.

Le code s’assure ici que le plus grand facteur de l’ordre de la courbe reste suffisamment grand (> 2^128) pour rester difficile à résoudre.

Quatrième vérification :

Un code similaire est exécuté:

n = E.order()
if n == p:
    beep_boop_error("My admins use safe curves!!!")
        return False

Ce code permet de contrer une attaque avec des anomalous curves.

Lorsque l’ordre de la courbe est égale à p, on dit que cette courbe est anomalous (anormale en francais). Elle est notamment vulnérable à l’attaque de Smart.

Cette attaque est assez implicite, elle utilise le lemme de Hensel pour lifter les points G et Q vers deux points G’ et Q’ d’un corp commutatif p-additique.

On résout ensuite le logarithme discret sur ces points puis on retrouve la solution dans Fp via la propriété isomorphique.

Cinquième est dernière vérification :

La dernière vérification est la suivante :

for k in range(1, 13):
    if (p^k - 1) % n == 0:
        beep_boop_error("Curve embedding degree is too small!!!!")
        return False

Il vérifie l’embedding de la courbe afin de prévenir de l’attaque MOV

Pour une courbe elliptique définie sur un corps fini Fp, le degré d’immersion k est le plus petit entier positif tel que l’ordre d’un point P de la courbe (souvent l’ordre du sous-groupe cyclique généré par P) divise p^k −1:

Le plus k tel que :

 $r | (q^k - 1)$

En termes plus simples, k est le plus petit entier pour lequel le corps de décomposition du sous-groupe de torsion du point P est

 $F_{ p^{k}}$

Ce corps est le plus petit corps sur lequel le sous-groupe de torsion du point P peut être entièrement représenté.

Pour des courbes aléatoires, on a souvent :

 $k \approx q$

mais pour les courbes super-singular, on a souvent:

 $k \leq 6$

Et de manière plus générale, il y a des familles de courbes avec

 $k \leq 50$

Cette attaque utilise-le "Weil paring" pour résoudre le logarithme discret dans un nouveau corps commutatif. Elle est souvent trés efficace car le logarithme discret est plus simple à résoudre dans

 $F_{ p^{k}}$

que dans

 $E(F_{ p})$

(quand k est petit)

Résolution du challenge :

Si on reprend le schéma de vérification d’une signature, on fournit (r, s) et effectue les calculs suivants :

 $z = H(m) \pmod{n} \newline w = s^{-1} \pmod{n}$

puis:

 $u_1 = zw \pmod{n} \newline u_2 = rw \pmod{n} \newline \newline X = u_1*G + u_2*Q \newline v = X.x \pmod{n} \newline$

et vérifie que v = s

Si on reprend la structure du challenge, on nous demande de signer un message avant même de fournir la courbe.
C’est une information très intéressante puisque cela nous permet de choisir une courbe pour ce message en particulier.

Dans le cas ou H(m) est égal à l’ordre de la courbe n. On a :

 $z = H(m) \equiv n \equiv 0 \pmod{n} \newline w = s^{-1} \pmod{n} \newline \newline u_1 = zw \equiv 0 \pmod{n} \newline u_2 = rw \pmod{n}$

De plus, en prenant r = s = Q.x, on a:

 $z = 0 \newline w = (Q.x)^{-1} \pmod{n} \newline \newline u_1 = 0 \newline u_2 = (Q.x) * (Q.x)^{-1} \equiv 1 \pmod{n} \newline \newline v = (u_1*G + u_2*Q).x \equiv Q.x \pmod{n}$

On peut vérifier de la manière suivante :

from Crypto.Util.number import getPrime

# Setup curve
p = getPrime(128)
E = EllipticCurve(GF(p), [-35, 98])
G = E.gens()[0]
d = randint(2, p - 1)   # Private key
Q = d * G               # Public key
n = E.order()           # Order of E

# Set Message to curve order
H = n

# Set r = s = Q.x
r = s = Q.xy()[0]

# ECDSA Verification
z = H % n
w = pow(s, -1, n)

u1 = int(z * w) % n
u2 = int(r * w) % n

X = (u1 * G) + (u2 * Q)

assert X[0] == r, 'Verification failed'
print('OK')

$ sage poc.sage
OK

Note :

On peut aussi utiliser :

 $r = 0$

s premier avec n pour satisfaire l’existence de son inverse

 $z = 0 \newline w = s^{-1} \equiv 1 \pmod{n} \newline \newline u_1 = zw \equiv 0 \pmod{n} \newline u_2 = rw \equiv 0 \pmod{n} \newline \newline v = (u_1*G + u_2*Q).x = O.x = 0 \newline$

Génération d’une courbe d’ordre H(m)

La première chose à faire est de s’assurer que H(m) est premier sinon il sera impossible de générer une courbe de cet ordre.

On peut de plus coder toute l’interface avec le challenge :

import os
os.environ['PWNLIB_NOTERM'] = '1'
from pwn import *
from hashlib import sha1
from re import findall

context.log_level = 'critical'

class client:
    def __init__(self, ip, port, debug):
        self.ip = ip
        self.port = port
        self.debug = debug

        if self.debug:
            self.io = process(['sage', 'server.sage'])
        else:
            self.io = remote(self.ip, self.port)

    def shell(self):
        self.io.interactive()

    def close(self):
        self.io.close()

    def get_hash(self):
        m = bytes.fromhex(self.io.recvline().decode().split(': ')[1])
        return int(sha1(m).hexdigest(), 16)

    def submit_curve(self, p, a, b):
        self.io.sendlineafter(b'= ', str(p).encode())
        self.io.sendlineafter(b'= ', str(a).encode())
        self.io.sendlineafter(b'= ', str(p).encode())

        Q = findall(r'\((.*?) : (.*?) :', self.io.recvline().decode())[0]
        return int(Q[0]), int(Q[1])

    def submit_sig(self, r, s):
        self.io.sendlineafter(b'= ', str(r).encode())
        self.io.sendlineafter(b'= ', str(s).encode())
        return io.recvline().decode()

def gen_curve_with_order(order: int) -> None:
    p = ...
    a = ...
    b = ...

    return p, a, b

while 1:
    c = client('<ip>', 1337, debug=True)

    m = c.get_hash()
    if not Integer(m).is_prime():
        c.close()
        continue

    p, a, b = gen_curve_with_order(m)
    Qx, Qy = c.submit_curve(p, a, b)

    result = c.submit_sig(r=Qx, s=Qx)
    print(result)

En se basant sur le papier Constructing Elliptic Curves of prime order de Bröker et Stevenhagen, ainsi que différents codes en ligne, on a ce code permettant de générer une courbe en spécifiant son ordre :

from sage.all import *

def generate_with_order(m, D=None, c=None):
    def generate_with_trace_q(t, q, D=None, c=None):
        def solve_cm(D, q, c=None):

            def hilbert_class_polynomial_roots(D, gf):
                assert D < 0 and (D % 4 == 0 or D % 4 == 1), "D must be negative and a discriminant"
                H = hilbert_class_polynomial(D)
                pr = gf["x"]
                for j in pr(H).roots(multiplicities=False):
                    yield j

            def generate_curve(gf, k, c=None):
                c_ = c if c is not None else 0
                while c_ == 0:
                    c_ = gf.random_element()

                a = 3 * k * c_ ** 2
                b = 2 * k * c_ ** 3
                return EllipticCurve(gf, [a, b])

            assert is_prime_power(q)

            gf = GF(q)
            if gf.characteristic() == 2 or gf.characteristic() == 3:
                return

            ks = []
            for j in hilbert_class_polynomial_roots(D, gf):
                if j != 0 and j != gf(1728):
                    k = j / (1728 - j)
                    yield generate_curve(gf, k, c)
                    ks.append(k)

            while len(ks) > 0:
                for k in ks:
                    yield generate_curve(gf, k, c)

        def is_square(x):
            y = isqrt(x)
            return y if y ** 2 == x else None    

        assert t ** 2 < 4 * q, f"Trace {t} is outside Hasse's interval for GF({q})"

        if D is None:
            D = t ** 2 - 4 * q
        else:
            assert (t ** 2 - 4 * q) % D == 0 and is_square((t ** 2 - 4 * q) // D), "Invalid values for t, q, and D."

        for E in solve_cm(D, q, c):
            if E.trace_of_frobenius() == t:
                yield E
            else:
                E = E.quadratic_twist()
                yield E

    factor_4m = factor(4 * m)

    def get_q(D):
        for t in set(map(lambda sol: int(sol[0]), pari.qfbsolve(pari.Qfb(1, 0, -D), factor_4m, 1))):
            if is_prime(m + 1 - t):
                return m + 1 - t
            if is_prime(m + 1 + t):
                return m + 1 + t

    q = None
    if D is None:
        for D in range(7, 4 * m):
            if not (D % 4 == 0 or D % 4 == 3):
                continue
            q = get_q(-D)
            if q is not None:
                break

        assert q is not None, "Unable to find appropriate D value for m."
        D = int(-D)
    else:
        q = get_q(D)
        assert q is not None, "Invalid values for m and D."

    yield from generate_with_trace_q(q + 1 - m, q, D, c)

Finalement, on peut assembler les deux codes afin de résoudre le problème:

import os
os.environ['PWNLIB_NOTERM'] = '1'
from pwn import *
from hashlib import sha1
from re import findall

from sage.all import *

context.log_level = 'critical'

class client:
    def __init__(self, ip, port, debug):
        self.ip = ip
        self.port = port
        self.debug = debug

        if self.debug:
            self.io = process(['sage', 'server.sage'])
        else:
            self.io = remote(self.ip, self.port)

    def shell(self):
        self.io.interactive()

    def close(self):
        self.io.close()

    def get_hash(self):
        m = bytes.fromhex(self.io.recvline().decode().split(': ')[1])
        return int(sha1(m).hexdigest(), 16)

    def submit_curve(self, p, a, b):
        self.io.sendlineafter(b'= ', str(p).encode())
        self.io.sendlineafter(b'= ', str(a).encode())
        self.io.sendlineafter(b'= ', str(b).encode())
        Q = findall(r'\((.*?) : (.*?) :', self.io.recvline().decode())[0]
        return int(Q[0]), int(Q[1])

    def submit_sig(self, r, s):
        self.io.sendlineafter(b'= ', str(r).encode())
        self.io.sendlineafter(b'= ', str(s).encode())
        return self.io.recvline().decode()

def gen_curve_with_order(m, D=None, c=None):
    def generate_with_trace_q(t, q, D=None, c=None):
        def solve_cm(D, q, c=None):

            def hilbert_class_polynomial_roots(D, gf):
                assert D < 0 and (D % 4 == 0 or D % 4 == 1), "D must be negative and a discriminant"
                H = hilbert_class_polynomial(D)
                pr = gf["x"]
                for j in pr(H).roots(multiplicities=False):
                    yield j

            def generate_curve(gf, k, c=None):
                c_ = c if c is not None else 0
                while c_ == 0:
                    c_ = gf.random_element()

                a = 3 * k * c_ ** 2
                b = 2 * k * c_ ** 3
                return EllipticCurve(gf, [a, b])

            assert is_prime_power(q)

            gf = GF(q)
            if gf.characteristic() == 2 or gf.characteristic() == 3:
                return

            ks = []
            for j in hilbert_class_polynomial_roots(D, gf):
                if j != 0 and j != gf(1728):
                    k = j / (1728 - j)
                    yield generate_curve(gf, k, c)
                    ks.append(k)

            while len(ks) > 0:
                for k in ks:
                    yield generate_curve(gf, k, c)

        def is_square(x):
            y = isqrt(x)
            return y if y ** 2 == x else None    

        assert t ** 2 < 4 * q, f"Trace {t} is outside Hasse's interval for GF({q})"

        if D is None:
            D = t ** 2 - 4 * q
        else:
            assert (t ** 2 - 4 * q) % D == 0 and is_square((t ** 2 - 4 * q) // D), "Invalid values for t, q, and D."

        for E in solve_cm(D, q, c):
            if E.trace_of_frobenius() == t:
                yield E
            else:
                E = E.quadratic_twist()
                yield E

    factor_4m = factor(4 * m)

    def get_q(D):
        for t in set(map(lambda sol: int(sol[0]), pari.qfbsolve(pari.Qfb(1, 0, -D), factor_4m, 1))):
            if is_prime(m + 1 - t):
                return m + 1 - t
            if is_prime(m + 1 + t):
                return m + 1 + t

    q = None
    if D is None:
        for D in range(7, 4 * m):
            if not (D % 4 == 0 or D % 4 == 3):
                continue
            q = get_q(-D)
            if q is not None:
                break

        assert q is not None, "Unable to find appropriate D value for m."
        D = int(-D)
    else:
        q = get_q(D)
        assert q is not None, "Invalid values for m and D."

    yield from generate_with_trace_q(q + 1 - m, q, D, c)

while 1:
    c = client('<ip>', 1337, debug=True)

    m = c.get_hash()
    if not Integer(m).is_prime():
        c.close()
        continue

    E = next(gen_curve_with_order(m))
    n = E.order()

    p = E.base().order()
    a = E.a4()
    b = E.a6()

    assert factor(n)[-1][0] >= 2^128
    assert n != p
    assert n == m

    Qx, Qy = c.submit_curve(p, a, b)

    result = c.submit_sig(r=Qx, s=Qx)
    print(result)

Et le flag final :

$ sage solve.sage
leHACK{I_have_lost_170M_x509_who_will_give_them_back?}

LostCertificate | Writeup challenge leHack2024 (Crypto)